Introducción
Las representaciones gráficas ayudan a visualizar y comprender los datos estadísticos de una forma muy directa.
Vamos a proponer tres tipos diferentes de gráficos estadísticos, compuestos de forma que puedan ser utilizados para representar multitud de datos de forma sucesiva sobre el mismo soporte.
Objetivo
El objetivo de esta actividad es que el alumno trabaje con distintos tipos de representaciones gráficas de datos próximos a su realidad. Mediante las tareas propuestas aprenderá a manejar las escalas del eje y se familiarizará con el concepto de variable y la utilización de instrumentos de medición: reglas y transportados de ángulos. Incluso para alumnos de cursos más avanzados se propone realizar un ajuste de escala mediante interpolación lineal.
Gráfico de barras
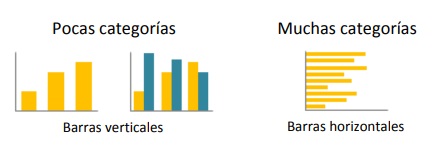
Los gráficos de barras se usan principalmente para comparar valores entre sí al colocar barras de igual grosor pero de longitud en proporción al valor que se está representando. Como orientación, se recomiendan emplear con el siguiente uso:
Se puede hacer un gráfico de barras con muchos materiales pero vamos a optar por un soporte de cartón pluma y velcro, para quitar y poner valores con facilidad.
Así, los materiales son los siguientes:
- Cartón pluma.
- Cartulina de color y blanca.
- Velcro.
- Tijeras.
- Pegamento.
Vamos a tomar como base un trozo de cartón pluma sobre el que irá nuestro gráfico. Las medidas dependerán del tamaño que queramos como resultado final. Debemos tener en cuenta que los ejes del gráfico y el título requieren de espacio suficiente en los márgenes.
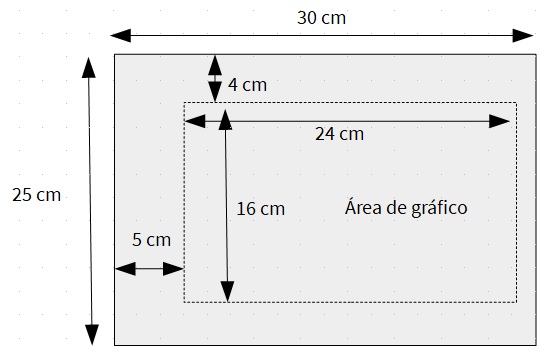
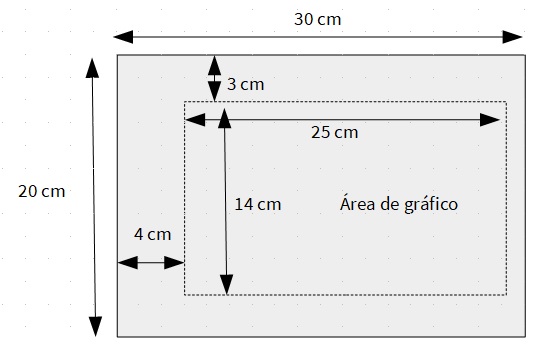
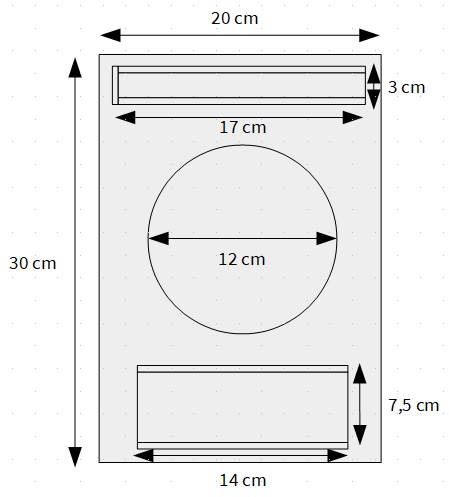
A modo de ejemplo, estas son las medidas de nuestro soporte para el gráfico:
Un sistema de velcro se queda pegado porque la parte de diminutos ganchos (la que pincha) se mezcla con la parte de pelo fino enroscado (la suave). Vamos cubrir todo el área de gráfico con la parte del velcro que pincha. Nuestro velcro es adhesivo, así que solo hay que pegar las tiras bien juntas para no dejar huecos. El ancho de cada tira de velcro es de 2 cm. Vamos a colocar 12 tiras (el motivo de que sean 12 es que ese es el número de meses que tiene un año y, como se verá con un ejemplo, nos interesa que podamos representar todos los meses).
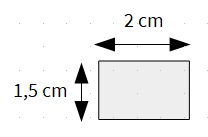
Adicionalmente, vamos a recortar otro trozo de cartón pluma de las medidas del área del gráfico y lo vamos a dividir en pequeños rectángulos. Dado que nuestras tiras de velcro tenían 2 cm de ancho, esa será la medida del ancho de nuestros rectángulos. Y como a las tiras de velcro le hemos dado 16 cm de alto, vamos a darle una medida de 1,5 cm para que con 10 rectángulos cubramos una tira sin que queden muy apretadas. Así, los rectángulos serían piezas de este tamaño:
Del mismo modo vamos a recortar rectángulos de la cartulina de color.
Ahora vamos a unir ambos tipos de rectángulos usando el pegamento. Y por el lado contrario a donde hemos puesto la cartulina de color, vamos a pegar la parte suave del velcro.
Ya tenemos las piezas con las que vamos a representar los datos en el gráfico de barras.
El siguiente paso va a consistir en hacer tres guías en las que introduciremos el nombre de la variable y la información de los dos ejes. Tenemos que pensar que hay que dejar un borde de 5 mm por tres de sus lados que se plegará para sujetar la cartela con la información correspondiente. El diseño sería así:
La guía del título de la variable no hace falta que sea muy ancha, pero las de los ejes sí necesitan un poco más de anchura para que tengan cabida las cifras y categorías que necesitemos poner:
Marcamos los bordes que vamos a plegar a lápiz, y cortamos los extremos del borde más pequeño (como se ve en la foto) para poder meterlos por debajo al pegar la guía en su sitio y que quede más firme.
El resultado quedaría así:
Notar que hemos usado una cartulina de color para que las guías se vieran bien en el ejemplo, pero unas guías blancas harían la misma función y pasarían más desapercibidas.
Ya solo queda definir los datos que vamos a representar, el título del gráfico y los valores de los ejes.
Como ejemplo, vamos a considerar como variable los meses en los que cumplen años los 25 alumnos de una clase.
Los datos que tenemos son los siguientes:
| Alumnos que cumplen años | |
|---|---|
| Enero | 2 |
| Febrero | 1 |
| Marzo | 3 |
| Abril | 2 |
| Mayo | 4 |
| Junio | 2 |
| Julio | 1 |
| Agosto | 1 |
| Septiembre | 2 |
| Octubre | 3 |
| Noviembre | 1 |
| Diciembre | 2 |
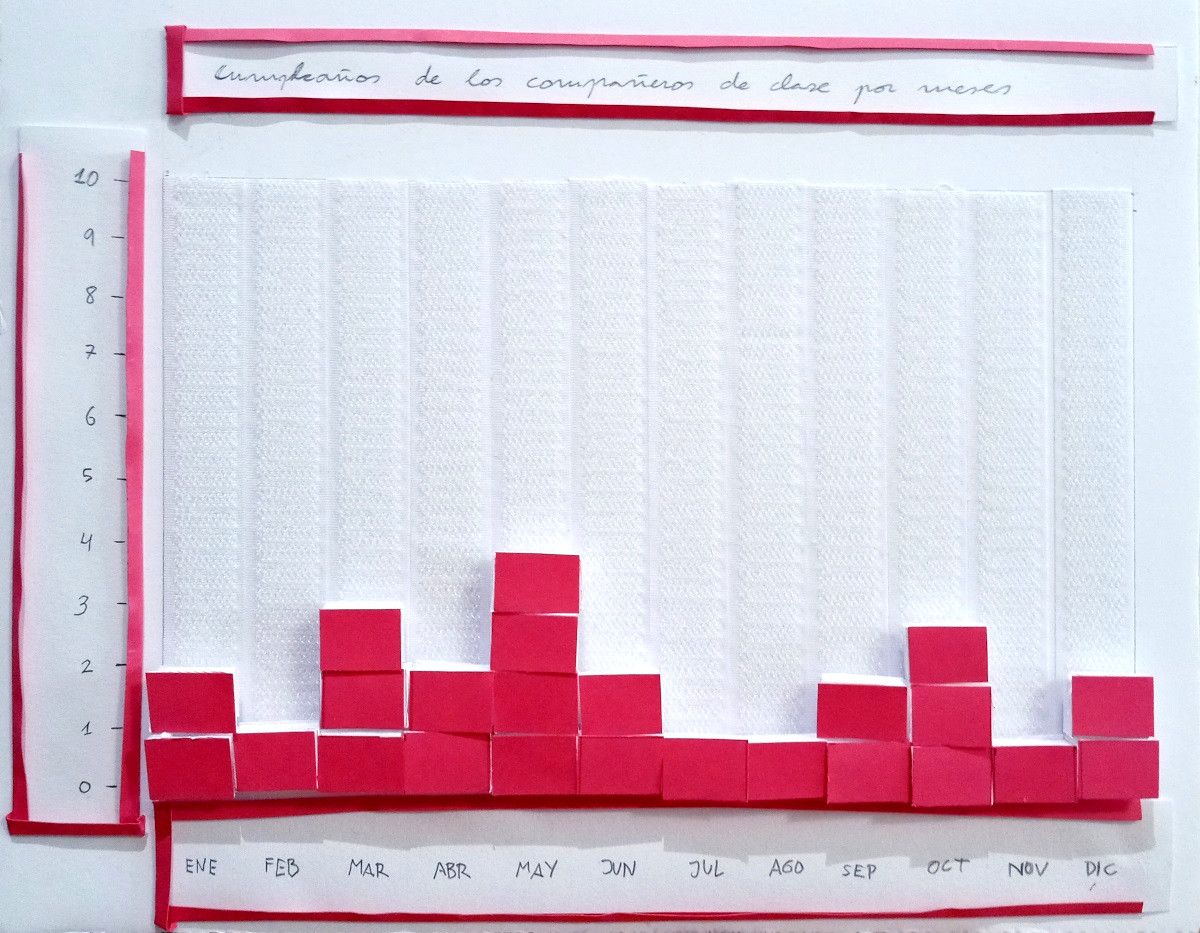
No se da la coincidencia de que más de 10 alumnos cumplan años el mismo mes, así que el eje Y llega hasta el 10. En el eje X ponemos todos los meses del año, abreviados para que quepan mejor, y en el título una descripción sencilla de qué estamos representando.
Ya podemos añadir rectángulos a nuestra representación en función de los datos:
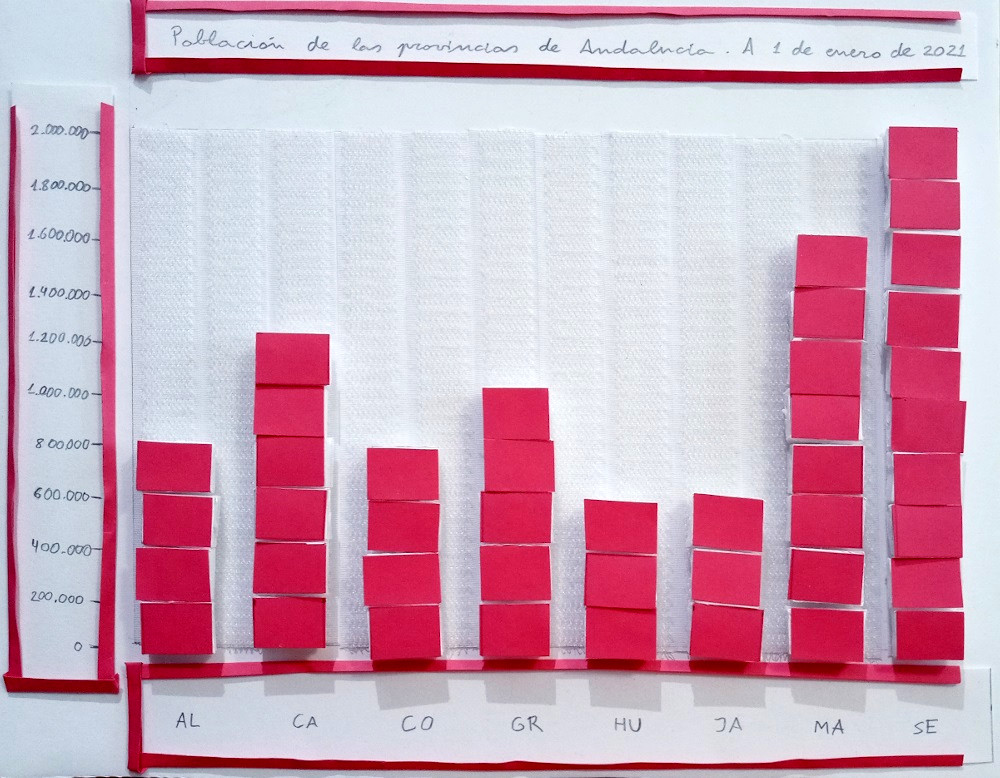
Vamos a ver otro ejemplo en el que tendremos que hacer una adaptación para poder representar datos con valores mucho más grandes. En este caso, la población de cada provincia andaluza a 1 de enero de 2021:
| Población | |
|---|---|
| Almería | 730.475 |
| Cádiz | 1.245.718 |
| Córdoba | 776.282 |
| Granada | 920.852 |
| Huelva | 524.613 |
| Jaén | 626.755 |
| Málaga | 1.694.089 |
| Sevilla | 1.946.452 |
Para aproximar estos datos a nuestro gráfico de bloques del 0 al 10, vamos a hacer una operación de interpolación lineal.
¿Qué es la interpolación lineal?
Consiste en trazar una recta entre dos valores conocidos y calcular los valores intermedios según esa recta.
Gráficamente se expresa así:
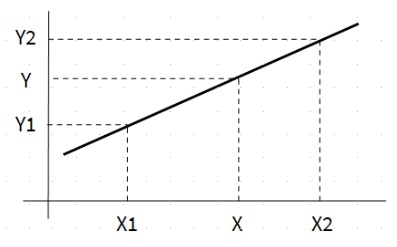
Mediante fórmula queda así:
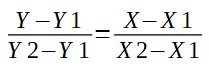
Conocemos todos los puntos menos el Y, de manera que despejando:
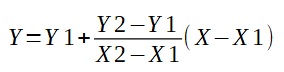
En nuestro ejemplo, como el valor mínimo que podemos representar es 0 rectángulos y el máximo son 10 rectángulos, Y1 = 0 e Y2 = 10.
La escala de los datos de población va a partir desde el 0 y llegará hasta los 2.000.000, ya que el valor máximo es 1.946.452, el de la población de Sevilla. Por tanto, X1 = 0 e X2 = 2.000.000. Por lo tanto, queda:
Ya solo hay que ir sustituyendo X por el valor de la población en cada provincia. Haciendo un redondeo de los resultados al número entero más próximo, tenemos los siguientes datos:
| Población | Rectángulos sin redondeo | Rectángulos con redondeo | |
|---|---|---|---|
| Almería | 730.475 | 3,7 | 4 |
| Cádiz | 1.245.718 | 6,2 | 6 |
| Córdoba | 776.282 | 3,9 | 4 |
| Granada | 920.852 | 4,6 | 5 |
| Huelva | 524.613 | 2,6 | 3 |
| Jaén | 626.755 | 3,1 | 3 |
| Málaga | 1.694.089 | 8,5 | 8 |
| Sevilla | 1.946.452 | 9,7 | 10 |
La representación después de la interpolación lineal quedaría así:
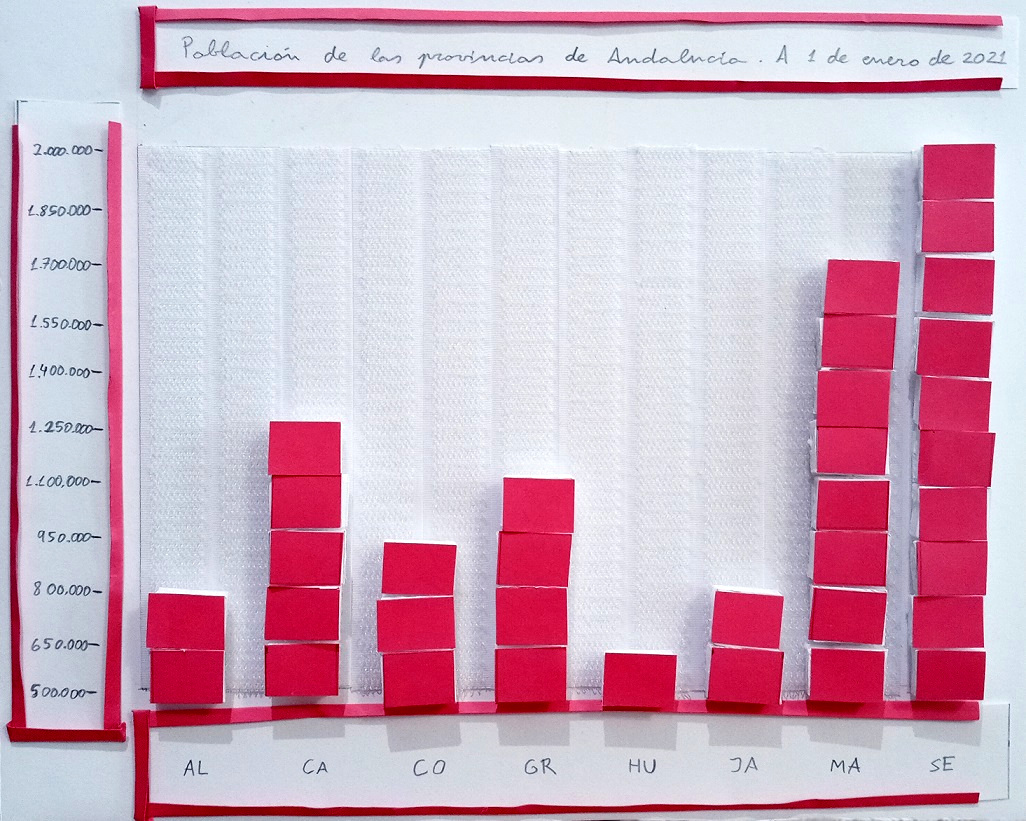
Podemos ajustar más la escala, y que así se vean más las diferencias entre las provincias, considerando Y1 = 1 y X1 = 500.000. De esta forma ponemos el límite inferior justo por debajo del menor valor, 524.613, el correspondiente a Huelva, y con Y1 = 1 nos aseguramos de que el valor más bajo salga representado con al menos 1 rectángulo.
El resultado con este cambio de escala es:
Gráfico de líneas
Los gráficos de líneas se utilizan habitualmente para ver la evolución de valores en el tiempo.
En este caso vamos a utilizar una base de corcho para poder pinchar los diferentes valores de una o varias series de datos. Los materiales son los siguientes:
- Corcho.
- Cartulina de color y blanca.
- Chinchetas de colores.
- Hilos gruesos de los mismos colores.
- Tijeras.
- Pegamento.
- Rotulador negro grueso.
A la hora de escoger el corcho y las chinchetas debemos tener en cuenta que las chinchetas no pueden sobresalir por el otro lado, o nos pincharemos con ellas. Una buena opción puede ser pegar el corcho a un trozo de tablero del mismo tamaño. Así nos aseguramos de que las chinchetas no van a traspasarlo y si éstas no llegan a clavarse del todo nos resultará más fácil luego añadir líneas con el hilo.
Estas son las medidas de nuestro soporte para el gráfico de líneas:
Vamos a construir las tres guías con cartulina de la misma forma que en los gráficos de barras.
En el área del gráfico vamos a dejar el corcho tal cual, pero vamos a marcar unas líneas punteadas con rotulador grueso que nos sirvan de referencia para colocar las chinchetas. Como tiene un alto de 14 cm, el espacio entre líneas será de 2 cm y el número de líneas 6.
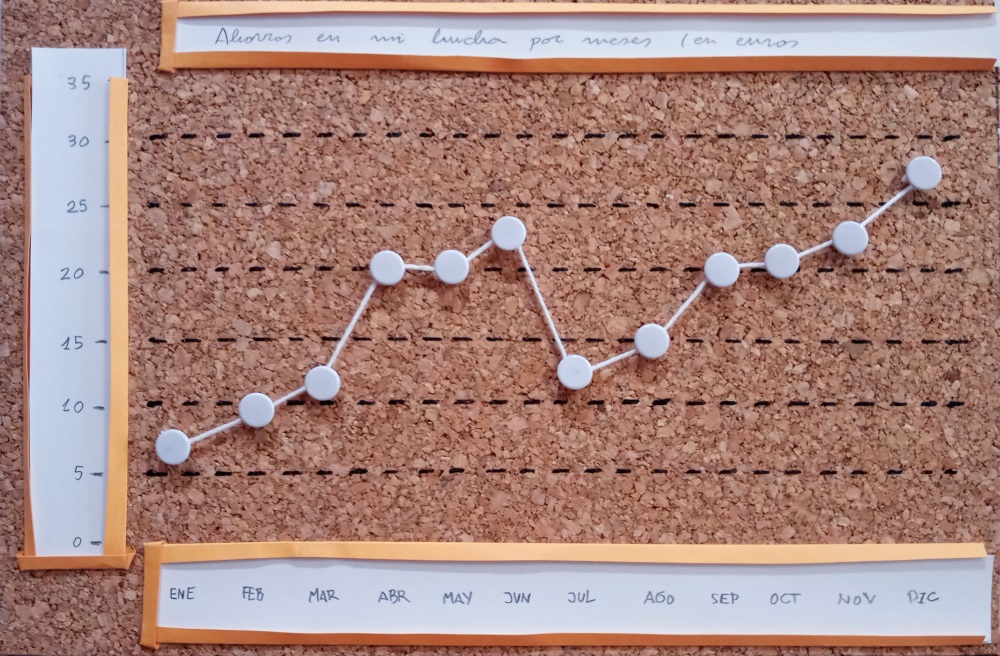
Los datos ficticios que vamos a representar como ejemplo serán los ahorros que se van acumulando en una hucha por meses. Vamos a clavar las chinchetas a la altura del valor en euros y del mes correspondiente:
Estos puntos con bastante clarificadores de cómo han ido evolucionando los ahorros de la hucha, pero podemos mejorar la representación incorporando un hilo del mismo color (el más apropiado sería un hilo de lana grueso que no tenga pelusa, para que la línea quede mejor definida). Con la incorporación de la línea quedaría así:
Solo hay que hacer un nudo en los puntos inicial y final, y darle una vuelta con el hilo a los puntos intermedios.
Podemos incorporar información adicional. En estos datos puede ser interesante marcar un objetivo del coste de lo que se tenga pensado comprar. O añadir etiquetas (de cartulina blanca para que se lean bien y queden rígidas) que expliquen fluctuaciones en los datos que se salen de lo normal.
En el mes de abril hay una subida significativa en el nivel de ahorros, se explica con una etiqueta “cumpleaños”, atribuible a un regalo en forma de dinero. El objetivo lo hemos marcado en 25 euros, con chinchetas e hilo rojo, que se sobrepasa en el mes de diciembre.
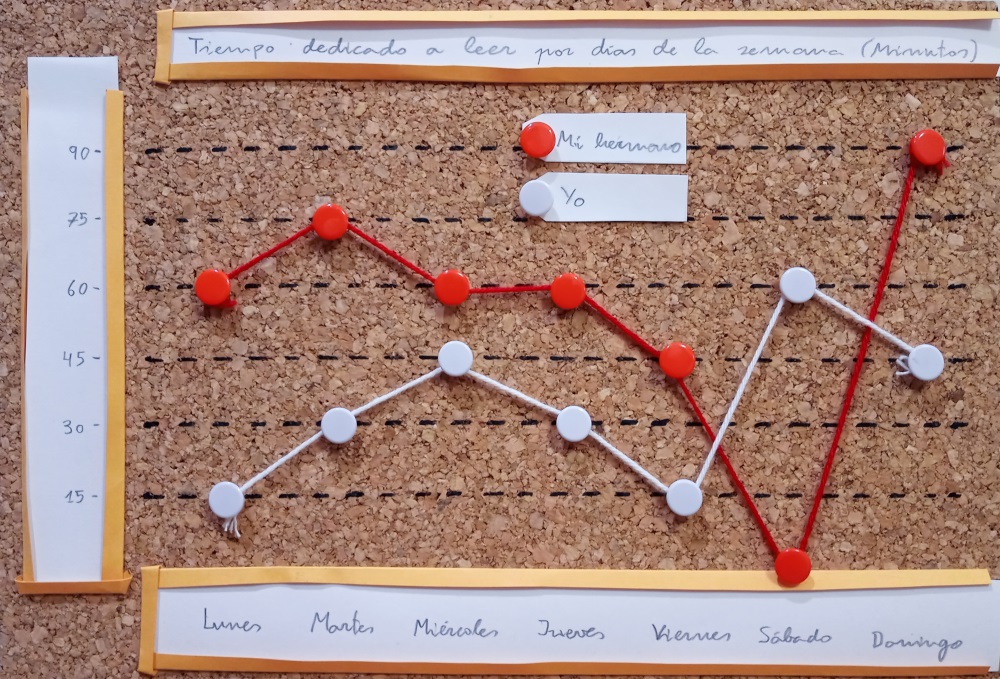
Podemos representar más de una serie de datos mediante este gráfico de líneas. Vamos a verlo con otro ejemplo. En esta ocasión representaremos el tiempo dedicado a leer (en minutos) por días de la semana. Una serie corresponde al alumno que ha hecho el gráfico (chinchetas e hilo de color blanco) y la otra a su hermano (chinchetas e hilo de color rojo). Para la leyenda usamos dos etiquetas de cartulina blanca.
Gráfico de sectores
Los gráficos de sectores se emplean cuando se quiere analizar la composición o distribución de unos datos.
Como en el gráfico de líneas, vamos a utilizar una base de corcho para poder definir el tamaño de los sectores con chinchetas e hilo. Los materiales son los siguientes:
- Corcho.
- Cartulina de color y blanca.
- Chinchetas e hilo de colores.
- Transportador escolar para medir ángulos.
- Tijeras.
- Pegamento.
- Rotulador negro grueso.
Al igual que con el gráfico de líneas, debemos tener cuidado con el grosor del corcho elegido y seguir las mismas recomendaciones.
Estas son las medidas del soporte para el gráfico de sectores, incluidas también las medidas de las dos guías que vamos a utilizar en este tipo de gráfico (una para el título y otra para la leyenda):
Para trazar el círculo vamos a usar un transportador escolar para medir ángulos. Con un lápiz lo vamos a fijar al centro y dando vueltas en torno a ese eje, trazaremos toda la circunferencia (ver la imagen siguiente) con un rotulador negro grueso.
Además, vamos a usar el transportador para definir unos ángulos que nos sirvan de referencia para marcar los porcentajes en el gráfico de sectores. Vamos a marcar los puntos que correspondan a porcentajes de 10 en 10 y de 25 en 25. Eso equivale a dividir los 360 grados de la circunferencia entre 10 y entre 4, respectivamente. Así, para los porcentajes del 10% habrá que hacer una marca cada 36 grados y para los porcentajes del 25% la marca será cada 90 grados (aunque coinciden en el 50% y el 100%).
Los transportadores de ángulos tienen un agujero que nos sirve para rotar el instrumento.
Esquema de los ángulos a marcar en el círculo:
Una vez dibujadas las referencias del círculo y pegadas las guías, pasamos a implementar unos datos de ejemplo.
Empezamos con uno muy sencillo: los porcentajes de niños y niñas en clase.
Se ha usado una chincheta en el centro desde la que parte el hilo hasta las otras, que marcan los valores de los porcentajes.
Las niñas representan el 44% y los niños el 56%, lo que se indica con etiquetas de cartulina y chinchetas de diferentes colores.
No tiene sentido usar la guía inferior para indicar la leyenda, ya que es un ejemplo muy sencillo. Sin embargo, se puede usar para incluir información adicional: cuántas personas hay en clase y cuántas son niñas o niños en valores absolutos.
Vemos otro ejemplo con más valores, uso del tiempo a diario con cuatro categorías: comer, dormir, jugar y colegio. Los porcentajes se indican de la misma forma que en el anterior, pero ahora usamos la guía inferior para señalar a qué corresponde cada color.
Te animamos a realizar esta actividad y a compartir con nosotros tus representaciones gráficas a través de nuestras redes sociales @IECA_Andalucia.